Keenan Crane*, Christina Vaz*, and Andreas Fabri°
*Carnegie Mellon University, °GeometryFactory
Measuring distances in space and over manifolds is one of the most fundamental operations
in geometry. More practically, computing accurate geodesic distances over triangulated
surface meshes is also crucial to a number of applications in geometry processing, such as
mesh parameterization, mesh segmentation, or mesh editing. However, although measuring distances
in space is usually easy, measuring intrinsic distances over triangulated surfaces accurately
is much more difficult.
Geodesic and Heat
Imagine touching a surface with a scorching hot needle. Over time heat will spread out from the contact point to the rest of the domain. This process can be described by a function called the heat kernel, which measures the heat transferred from a source to a destination after a given time. A well-known relationship between heat and distance is Varadhan’s formula, which says that the geodesic distance between any pair of points on a Riemannian manifold can be recovered via a simple pointwise transformation of the heat kernel.
The Heat Method
The heat method is an algorithm that solves the single- or multiple-source shortest path problem by returning an approximation of the geodesic distance for all vertices of a triangle mesh to the closest vertex in a given set of source vertices. It was introduced in a paper published at the ACM SIGGRAPH conference in 2017, and co-authored by Keenan Crane, Clarisse Weischedel, and Max Wardetzky, and uses the heat kernel to compute geodesics, following an approach illustrated in the figure below.
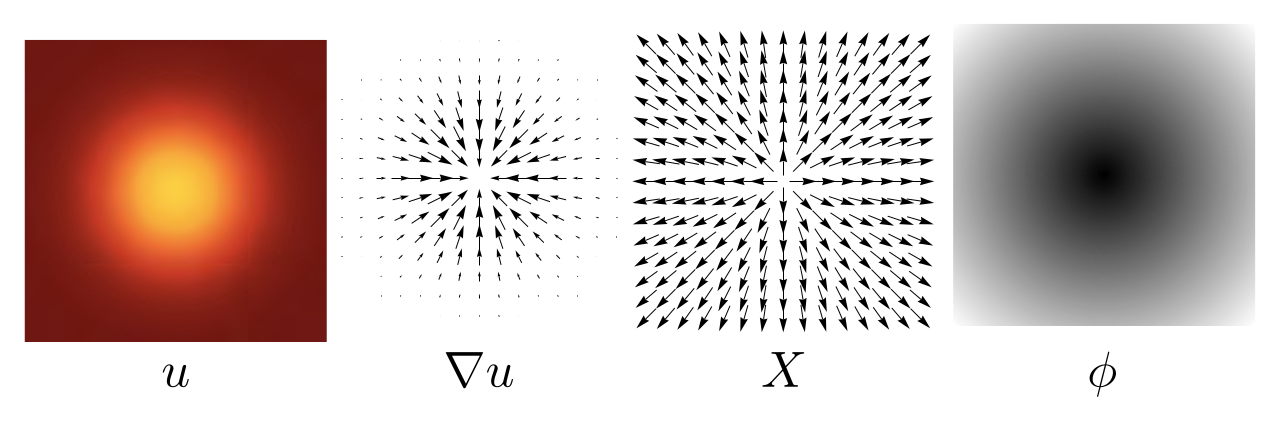
Outline of the heat method. (I) Heat is allowed to diffuse for a brief period of time (left). (II) The temperature gradient (center left) is normalized and negated to get a unit vector field (center right) pointing along geodesics. (III) A function whose gradient follows the vector field recovers the final distance is computed (right) [1].
The heat method is highly efficient since the algorithm boils down to two standard sparse linear algebra problems. It is especially useful in situations where one wishes to perform repeated distance queries on a fixed domain, since precomputation done for the first query can be re-used.
Heat Method : The Package
The newest CGAL package, Heat_method_3 implements the heat method. This package is related to the package Triangulated Surface Mesh Shortest Paths as both deal with geodesic distances. The heat method package computes for every vertex of a mesh an approximate distance to one or several source vertices, whereas the geodesic shortest path package computes the exact shortest path between any two points on the surface.

Geodesic distance on the Stanford Bunny. The heat method allows distance to be rapidly updated for new source points or curves. [1]
The package Heat_method_3 is the result of the work of Christina Vaz during the 2018 season of the Google Summer of Code, mentored by Keenan Crane and Andreas Fabri. It is now available in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL (4.14) scheduled for March 2019.