Cédric Portaneri*, Mael Rouxel-Labbé°, Michael Hemmer, David Cohen-Steiner*, Pierre Alliez*
*INRIA Sophia Antipolis, °GeometryFactory
Surface meshes are essential components in the majority of geometry processing and computer graphics applications such as segmentation, remeshing, or simulation. The feasibility of an operation and the quality of the results often depend on the validity and the quality of the mesh. For these reasons, most applications require --- or prefer --- input meshes that are valid, i.e., watertight, combinatorially 2-manifold and orientable, as these properties imply well-defined notions of interior/exterior and geodesic neighborhoods. Despite the crucial role played by meshes, many mesh generation processes (manual design by humans, automated generation from flawed CAD models, reconstruction from measurement data, ...) remain imperfect and can be responsible for a wide variety of possible defects in meshes: duplicates, degeneracies, holes and gaps, self-intersections, non-manifold features or inconsistent orientation. These defects generally compound into critical issues such as inconsistent boundary representations of the object they are supposed to model, significantly hampering further operations.
The 3D Alpha Wrapping Package
With the next CGAL release, a new package will address the problem of generating a watertight and orientable surface triangle mesh from a given defect-laden input. In addition to validity, our method produces an output that strictly encloses the input. Such an enclosing property is mandatory for applications related to conservative distance queries, collision avoidance, or motion planning.
The method is fast, proven to terminate, and generic to the input data representation (triangle meshes, soups, segments, points, ...).
Algorithm
The core idea behind our approach is to detach the structure being carved from the input geometry: instead of carving a triangulation whose vertices are points of the input, as it is the case in sculpting methods, we start from an entirely new and coarse enclosing mesh, and interlace carving and refinement steps to create the final approximation.
Our algorithm is carving operates on an underlying 3D Delaunay triangulation whose tetrahedral cells are tagged inside or outside, and the resulting surface mesh is defined as the set of Delaunay facets separating inside from outside Delaunay cells. The carving step trims the mesh inward by tagging outside a Delaunay cell that was formerly tagged inside. The refinement step is triggered when an upcoming carving step would expose the input geometry, i.e., when the tetrahedron cell that is to be tagged outside actually intersects the input. In this configuration, carving is not performed and a Steiner point is instead inserted into the Delaunay triangulation to refine the tetrahedron cell. The Steiner points added during refinement operations do not lie directly on the input but rather on the offset surface, which is defined as a level-set of the unsigned distance field to the input. More specifically, a Steiner point is computed either as the intersection of a dual Voronoi edge with the offset surface, or as the projection of the circumcenter of a Delaunay cell onto the offset surface. Intuitively, our method is devised to allocate on-demand new degrees of freedom for carving, in a manner that favors low output complexity and well-shaped elements. The figure below illustrates our algorithm at work in 2D on a soup of line segments characterized by many defects such as intersections, gaps, and non-manifold features.
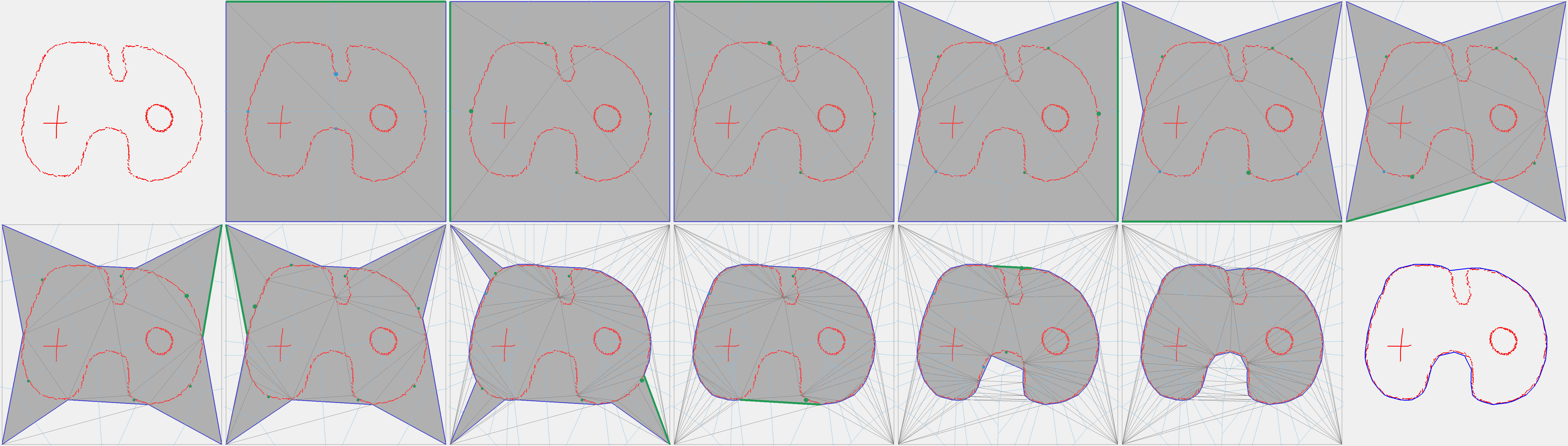
Illustration of the algorithm in 2D. Input (red) and a few steps of the algorithm (click to enlarge).
Usage
Two parameters control the behavior of our algorithm: alpha and offset. The parameter alpha controls the minimum carving size, and thus the size of straits and holes that cannot be traversed during carving. The parameter \delta is the value of the distance field level-set defining the offset surface. It controls the distance of the mesh vertices to the input, and thus the tightness of the approximation (see Figure below). Both parameters can be chosen independently and arbitrarily large or small, but must be strictly positive.

Multiple wrappings of the bike model for various combinations of alpha and offset (click to enlarge).
Alpha and offset impact the complexity-fidelity tradeoff.
Robustness
Our algorithm combines Delaunay refinement and carving techniques. Using these extendedly studied techniques and data structures enabled us to create a method that is proven to terminate and satisfy a number of conditions (validity, manifoldness, output encloses the input).
Genericity
Our algorithm is made generic by using an oracle class whose role is to answer a number of geometric queries (such as "What is the distance between this 3D point and the input data?"). The oracle's API is fixed and as such it is possible to easily switching input representations by simply replacing one implementation of oracle - and thus one type of input data - by another. In our implementation, we have even added the possibility to combine oracles; consequently, different input representations can be mixed together in the same scene queried by the oracle. The figure below illustrates such a setting on the blade model, where we compute the alpha wrap on input data that combine points, polylines, and triangles.

Single wrap of input data with different representation types: points, segments, triangles (click to enlarge).
Status
The package Alpha_wrap_3 is already integrated in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL, CGAL 5.5, scheduled for June 2022.
Documentation of the package Alpha_wrap_3
CGAL master branch on GitHub
