New in CGAL: 3D Periodic Mesh Generation

Mikhail Bogdanov*, Aymeric Pellé*, Mael Rouxel-Labbé°, and Monique Teillaud*

*INRIA, °GeometryFactory

The field of algorithmic geometry is traditionally limited to Euclidean spaces. Consequently, this is also the case for most data structures and algorithms in CGAL. However, by assuming other geometric postulates, it is possible to consider different kinds of spaces, such as periodic spaces defined as the quotient of an Euclidean space with an associative group, also known as flat torus. In a simpler-to-visualize way, such periodic spaces can been seen as a square (in 2D) or cubic (in 3D) tile that paves the Euclidean space. Geometric entities living in these spaces are duplicated across all tiles.

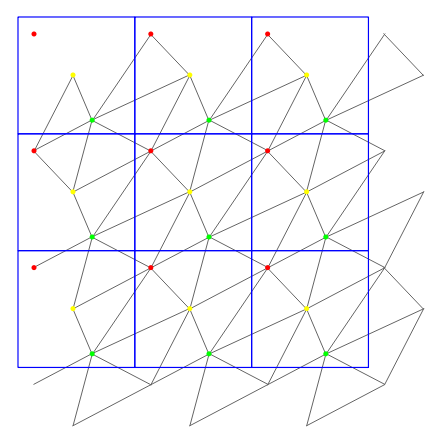
Example of 3 points in a 2D periodic space: the points and simplicies are reproduced periodically from tile to tile.

These periodic spaces are particularly well adapted to materials science and the modelling of some physic phenomena such as crystallographic structures, the cosmic web, and more (see for example, the program of the CGAL Prospective Workshop on Geometric Computing in Periodic Spaces )... As in the Euclidean space, the study of these topics requires discretizing objects in triangulations and meshes. The construction of 3D periodic triangulations has been available in CGAL since CGAL 3.5, with the release of the package 3D Periodic Triangulations. The next natural step was to offer mesh generation, that is the automatic generation of new points of a triangulation to construct a good approximation of a given domain living within the periodic cube.

3D Periodic Mesh Generation

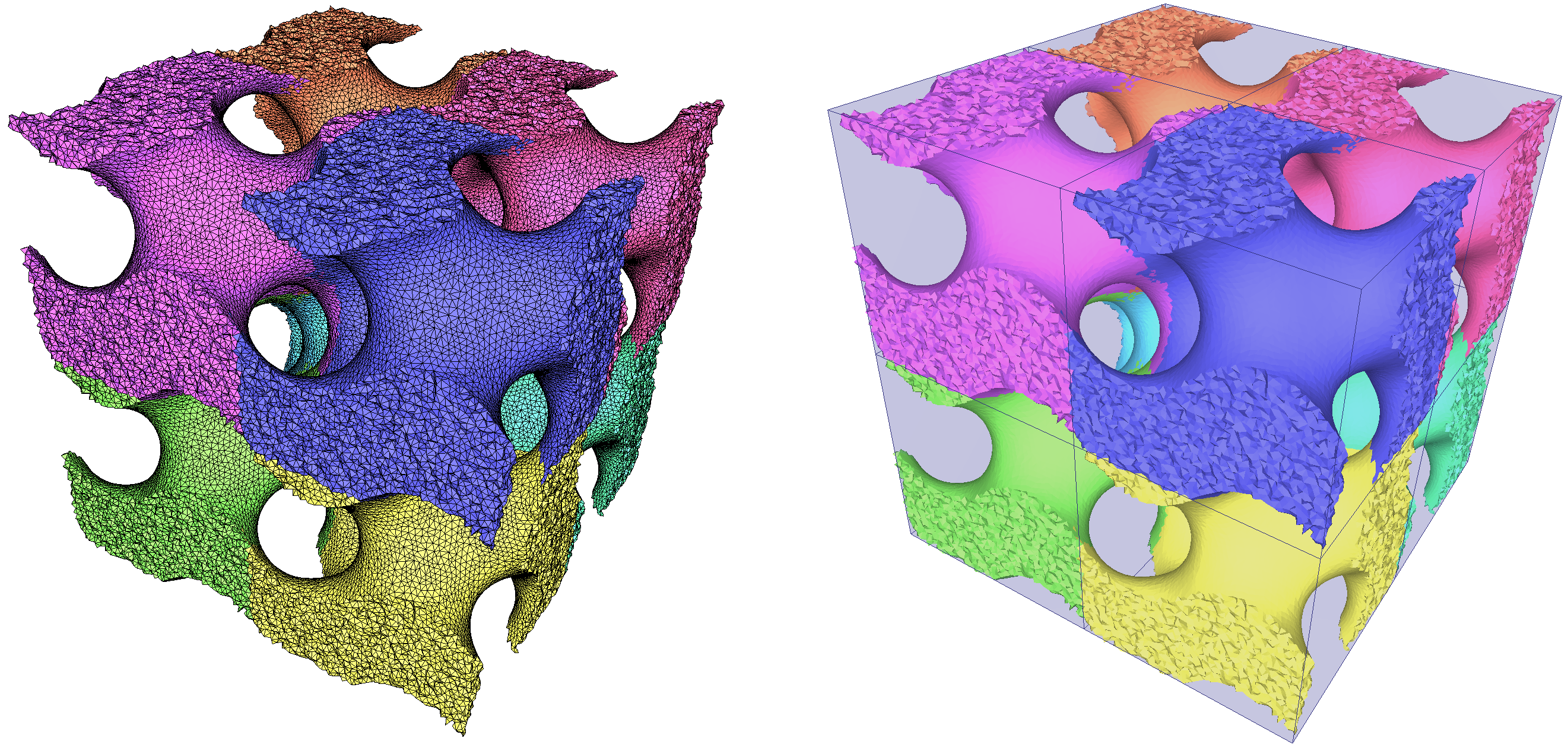
Introducing the newest CGAL package: 3D Periodic Mesh Generation (also known as Periodic_3_mesh_3). The package Periodic_3_mesh_3 computes isotropic simplicial meshes for domains described through implicit functional boundaries over the flat torus. The output is a periodic 3D mesh of the domain volume and conformal surface meshes for all the boundary and subdividing surfaces.

Example of a periodic mesh (8 representations of the mesh are shown, each with a different color).

The package is closely related to the 3D Mesh Generation package (also known as Mesh_3), with similar concepts, classes, and API. The package Periodic_3_mesh_3 therefore also offers feature protection, to ensure the presence of sharp edges in a mesh, as well as post-processing steps such as mesh optimization (Lloyd, ODT, sliver removal, ...):

Optimization of a periodic mesh (8 representations shown).

The package Periodic_3_mesh_3 is already integrated in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL, CGAL 4.13, scheduled for September 2018.