New in CGAL: Triangulated Surface Mesh Approximation

Pierre Alliez*, David Cohen-Steiner*, and Lingjie Zhu°

*INRIA, °National Laboratory of Pattern Recognition

For many applications ranging from reverse engineering to computational engineering, constructing concise and faithful approximations of excessively verbose 3D data sets (in particular, scanned meshes) is beneficial for subsequent processing and may reduce the computational cost dramatically.

Large scanned data sets, such as Standford's Lucy statue are good candidates of inputs that can greatly benefit from approximation.

Ideally, each element should be made as efficient as possible by stretching it locally in order to fit a large area of the shape to be approximated, while minimizing geometric error. This quest for geometric efficiency naturally raises the following question: given a 3D surface, a target number of face elements, and an error metric, what is the best geometric approximation of the object that one can find with this face budget? Or similarly, given a distortion tolerance, what is the smallest polygonal mesh approximant with a distortion lesser than the tolerance?

Triangulated Surface Mesh Approximation

Introducing the newest CGAL package: Triangulated Surface Mesh Approximation. This package implements the Variational Shape Approximation (VSA) method, introduced in a paper published at the ACM SIGGRAPH conference in 2004, and co-authored by David Cohen-Steiner, Pierre Alliez, and Mathieu Desbrun.

The VSA technique leverages a discrete clustering algorithm to approximate the input data by a set of local simple shapes referred to as proxies. Each cluster is represented as a connected set of triangles of the input mesh, and the output mesh is constructed by generating a surface triangle mesh which approximates the clusters.

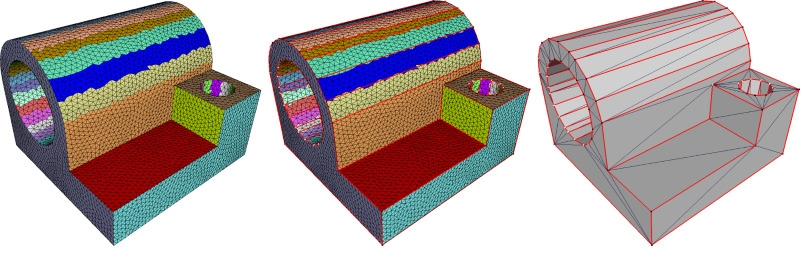
Partition of the input surface triangle mesh (left), extraction as a polyhedral mesh (middle), and final output triangle mesh (right). The partition is optimized via discrete clustering of the input triangles, to minimize the approximation error from the clusters to the planar proxies (not shown).

The approximation error is one-sided, defined between the clusters and their associated proxies, based on a user-chosen (or even user-defined) metric. The current proxies are planes or vectors, however the algorithm design is generic for future extensions to non-planar proxies.

The shape approximation algorithm distributes mesh elements according to local surface complexity. On the right, a flat-shaded comparison between original model and its 5K vertex polygonal approximation shows good preservation of the shape and of its highlights [1].

Apart from mesh approximation, this package can also be seen as providing a new tool for mesh simplification, or as a complement to the existing mesh segmentation package.

The package Triangulated Surface Mesh Approximation is the result of the work of Lingjie Zhu during the 2017 season of the Google Summer of Code, mentored by Pierre Alliez. It is now available in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL (4.14) scheduled for March 2019.