Iordan Iordanov and Monique Teillaud
INRIA Nancy - Grand Est, LORIA
Delaunay triangulations are among the most important structures in computational geometry and have been part of CGAL since its very first release. However, they are traditionally only handled in Euclidean spaces. Recent developments in fields such as neuromathematics, physics, material sciences, and computer modeling however exhibit needs for Delaunay triangulations in other spaces. CGAL already offers packages to compute Delaunay triangulations of the flat torus in 2 and 3 dimensions, which can be seen as periodic triangulations of the Euclidean space in 2 and 3 dimensions, respectively. CGAL introduces now two new packages for the computation of Delaunay triangulations in the hyperbolic plane, as well as Delaunay triangulations of the Bolza surface, which can be seen as periodic Delaunay triangulations of the hyperbolic plane.
2D Hyperbolic Triangulations
The hyperbolic plane is represented using the conformal Poincaré disk model. The package 2D Hyperbolic Triangulations (also known as Hyperbolic_triangulation_2) enables the computation of Delaunay triangulations of points living in the Poincaré disk. Further operations supported are the location of a point in the triangulation, the removal of existing vertices, and the computation of dual objects of faces and edges.
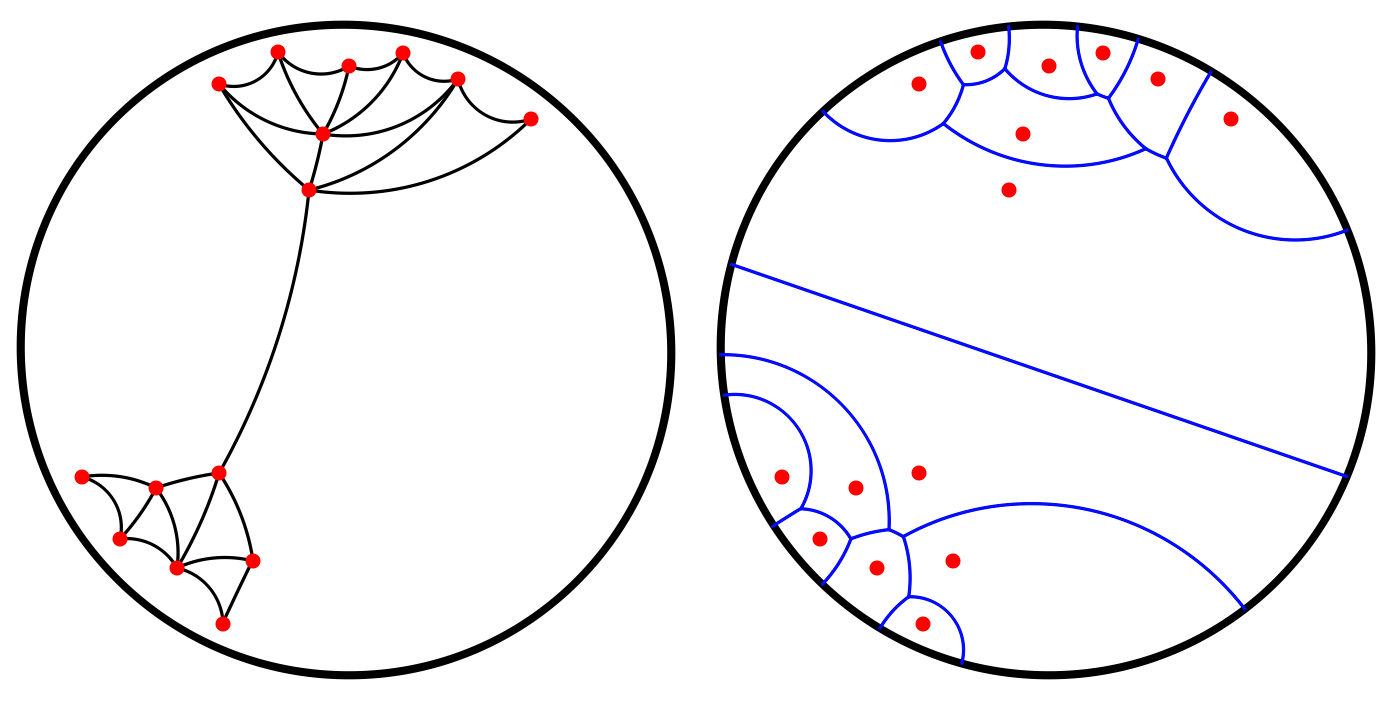
Delaunay triangulation and Voronoi diagram of a set of points on the Poincaré disk.
2D Periodic Hyperbolic Triangulations
The Bolza surface is the most symmetric smooth, closed, orientable surface of genus 2. It can be obtained by gluing together the opposite sides of a regular hyperbolic octagon with all angles equal to π/4. Note that this octagon tiles the hyperbolic plane. Delaunay triangulations of the Bolza surface can be seen as Delaunay triangulations of the hyperbolic plane, periodic in the 4 directions defined by the gluing of the opposite sides of the octagon.
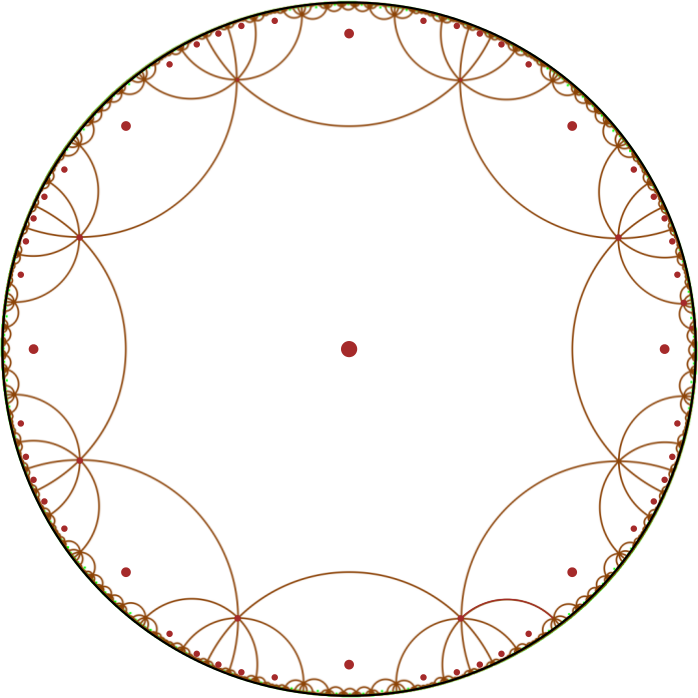
Illustration of the periodicity of the hyperbolic plane. All the red points correspond to the same point, periodically reproduced.
The package 2D Periodic Hyperbolic Triangulations (also known as Periodic_4_hyperbolic_triangulation_2) enables the computation of periodic Delaunay triangulations of the hyperbolic plane, and offers functionalities such as point location, vertex removal, and construction of dual objects of faces and edges of the triangulation.
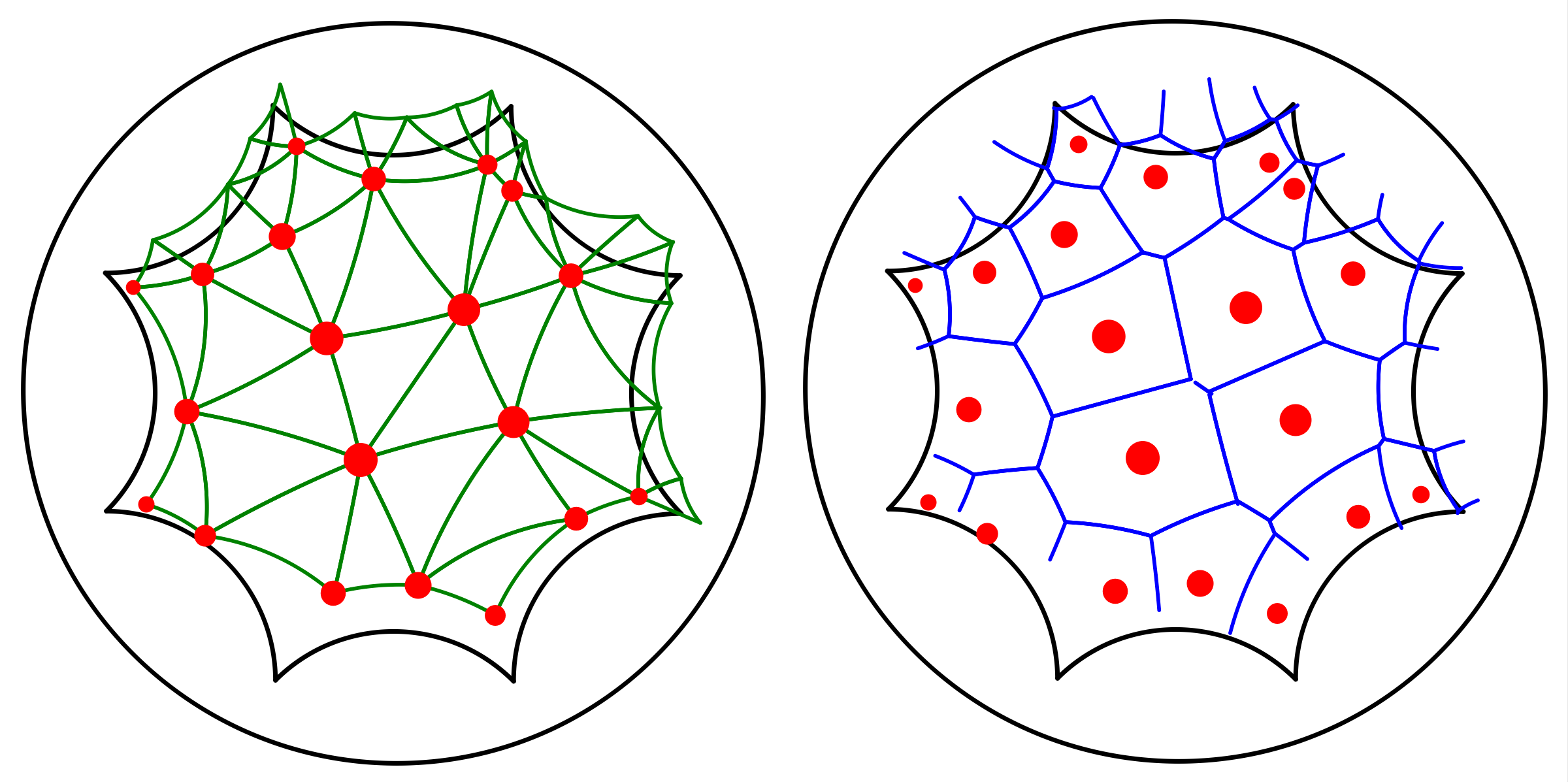
Periodic Delaunay triangulation and periodic Voronoi diagram of a set of points.
Both packages are already available in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL, 4.14, scheduled for March 2019.
Documentation of the package Hyperbolic_triangulation_2
Documentation of the package Periodic_4_hyperbolic_triangulation_2