Ken Arroyo Ohori*, Andreas Fabri°, and Sébastien Loriot°
*TU Delft, °GeometryFactory
Polygons are one the standard representations of geometric data, and are extensively used in various fields, and in particular visualisation and Geographic Information Systems (GIS). Within CGAL, 2D polygons (possibly with holes) are used in various packages such as 2D Polygon Partitioning, 2D Straight Skeleton and Polygon Offsetting, 2D Minkowski Sums, 2D Polyline Simplification, or 2D Visibility Computation. Whether for CGAL or external algorithms, a valid polygon is generally required as input. Unfortunately, although the validation of polygons has now been comprehensively studied, sanitization of error-laden inputs has received much less attention, and no solution existed within CGAL until recently.
The package 2D Polygon Repair is one the lastest additions to CGAL, and provides automatic repair of invalid polygons with a fast and generic implementation, with immediate compatibility with other polygon-based CGAL packages.
A Triangulation-based Approach to Automatic Polygon Repair
This new package implements different polygon repair methods. Starting from possibly invalid inputs in the form of a polygon, polygon with holes or multipolygon with holes, the method computes an arrangement of the input edges, labels each face according to what it represents (exterior, polygon interior, or hole), and reconstructs the polygon(s) represented by the arrangement. The method returns valid output stored in a multipolygon with holes, and calling it as simple as:
...
std::ifstream in("data/bridge-edge.wkt");
CGAL::Polygon_with_holes_2<Kernel> pwh;
CGAL::IO::read_polygon_WKT(in, pwh);
Multipolygon_with_holes_2 mp = CGAL::Polygon_repair::repair(pwh);
...
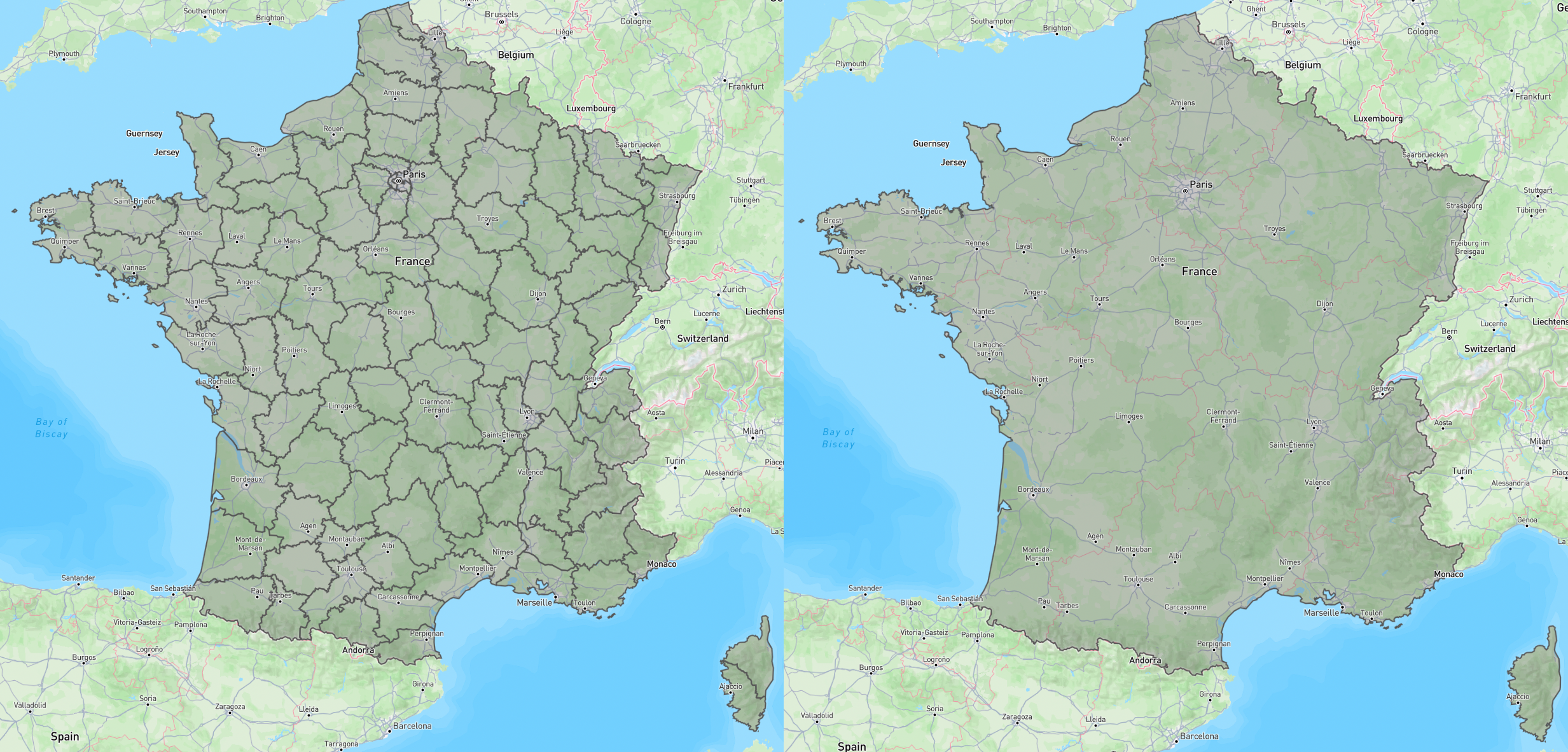
Turning the multipolygon of metropolitan french departments into two polygons using the non-zero rule
Repair Strategies
For a given invalid polygon inputs, multiple solutions might exist. Consequently, different labeling heuristics are possible. Four strategies are currently offered by the new package:
- the even-odd rule. In this strategy, areas are alternately assigned as polygon interiors and exterior/holes each time that an input edge is passed. It does not distinguish between edges that are part of outer boundaries from those of inner boundaries;
- the non-zero rule, which keeps areas with a non-zero winding number;

Input (left), non-zero (middle) even-odd (right).
- the union rule, which keeps areas that are contained in at least one of the input polygons (with holes);
- the intersection rule, which keeps areas that are contained in all input polygons (with holes).

Union (top) and Intersection (bottom).
The choice of strategy will generally depend on the input polygon type, and on the downstream application(s). For example, the "union" and "intersection" rules are useful when given two or more similar valid polygons with holes or to obtain an approximation from outside and inside.
Status
The initial CGAL 6.0 implementation of the Polygon Repair package providing only the "even-odd" rule was the result of a successful Google Summer of Code project, contributed by Ken Arroyo Ohori mentored by Andreas Fabri and Sébastien Loriot, and based on the work of Ledoux, Ohori, and Meijers [1]. Non-zero, union, and intersection strategies were added in CGAL 6.1 by Andreas Fabri.
All these additions are already integrated in CGAL's master branch on the CGAL GitHub repository. Polygon repair has been available since CGAL 6.0, and the new even-odd rule as well as the Boolean operations will be officially released in the upcoming version of CGAL, CGAL 6.1, scheduled for mid 2025.
Documentation of the “2D Polygon Repair” package
CGAL master branch on GitHub
Bibliography
[1] Ledoux, H., Ohori, K. A., & Meijers, M. (2014). A triangulation-based approach to automatically repair GIS polygons. Computers & Geosciences, 66, 121-131.