New in CGAL: New Surface Remeshing Algorithms

Sébastien Loriot, Sébastien Valette, and Hossam Mohamed Saeed

Numerous tasks in geometric modeling and processing revolve around 3D geometric objects represented by surface meshes. Such meshes can be created through different processes (CAD, scans, ...), with varying element shape and size, which might not be adapted to downstream applications. For example, 3D scanners can create amounts of data that are excessive for a simple visualization. Adapting the density of the mesh, also known as remeshing, is thus a crucial step to fit the data to application needs.

CGAL offers various packages and functions that can be used to construct a mesh from scratch, resample a mesh, or adapt the mesh to a set of criteria, notably:

• CGAL::Polygon_mesh_processing::surface_Delaunay_remeshing(), which remeshes a surface triangle mesh following a Delaunay refinement algorithm.
• CGAL::Polygon_mesh_processing::isotropic_remeshing(), which uses atomic operations such as edge splits, edge collapses, edge flips, and Laplacian smoothing to adapt a mesh to a user-provided sizing field.
• Triangulated Surface Mesh Simplification, which regroups a family of methods that can be used to progressively prune a mesh using for example quadric error metrics.

Recently, two new methods have been introduced to CGAL, with the purpose of generating coarser versions of surface meshes:

• Approximated Discrete Centroidal Voronoi Diagram (ACVD) Remeshing, which can be used to create high-quality feature-preserving surface meshes with a user-provided budget of vertices.
• Almost Planar Face Remeshing, to be used when one desires to extract the coarsest possible mesh without sacrificing geometry.

Approximated Discrete Centroidal Voronoi Diagram (ACVD) Remeshing

The function CGAL::Polygon_mesh_processing::approximated_centroidal_Voronoi_diagram_remeshing() uses clustering on polygonal meshes as to approximate a Centroidal Voronoi Diagram construction. It is inspired by the method introduced by Valette and Chassery [1] and further developed by Audette et al. [2] and Valette et al. [3]. The algorithm is similar to Lloyd's algorithm (or k-means), where random input vertices are picked to initialize clusters of vertices, which are then grown to minimize a particular energy, until convergence. Upon convergence, output vertices are computed from the vertices of each cluster. The algorithm combines the robustness and theoretical strength of Delaunay criteria with the efficiency of entirely discrete geometry processing, with a low complexity (in terms of calculations and memory requirements), allowing the processing of large meshes up to several million triangles.

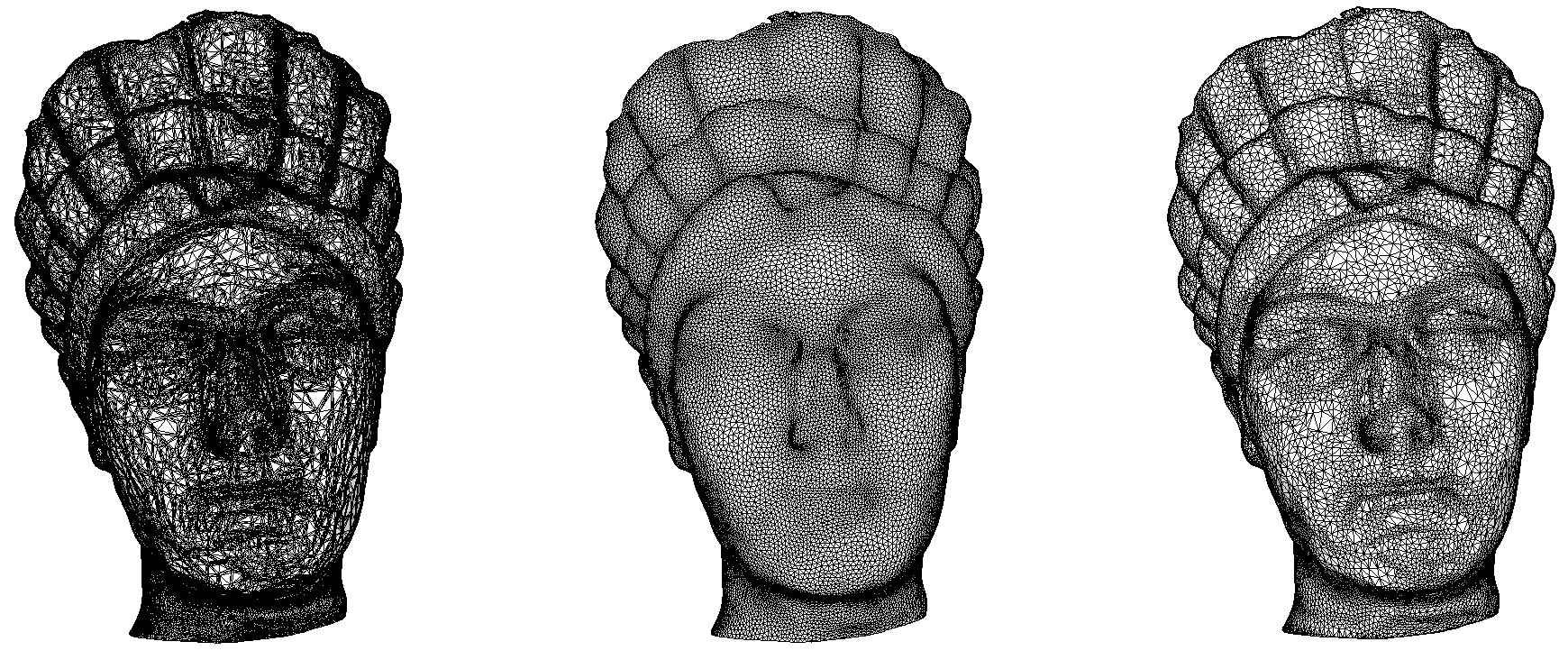
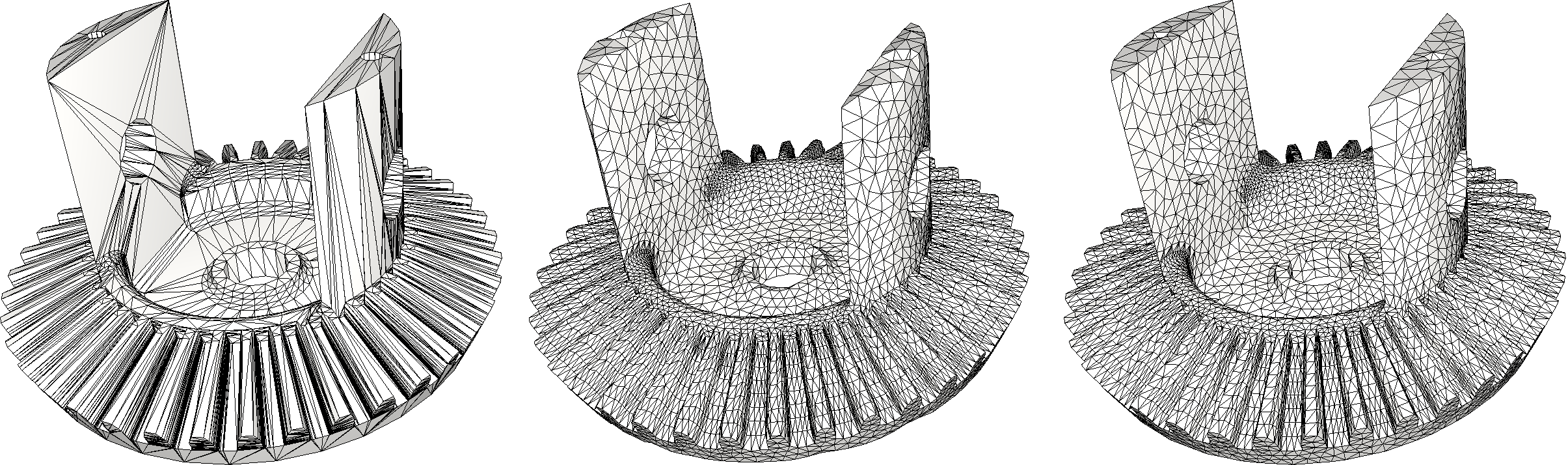
Input (left); remeshing with a budget of 50k vertices: isotropic (middle) and curvature adapted (right).

If the input mesh contains sharp features or corners, it is possible to use quadric error metrics to either move output vertices (fast, but can produce bad looking triangles), of to use quadric error metrics directly into the energy formulation of each cluster (slower, but produces better quality triangles). Additionally, adaptive remeshing based on surface curvature is possible.

Input (left); remeshing without (middle) and with (right) QEM-based placement optimization.

This implementation of the ACVD Remeshing method was the result of another successful Google Summer of Code project in CGAL, contributed by Hossam Saeed mentored by Sébastien Valette and Sébastien Loriot.

Remeshing of (Almost) Planar Patches

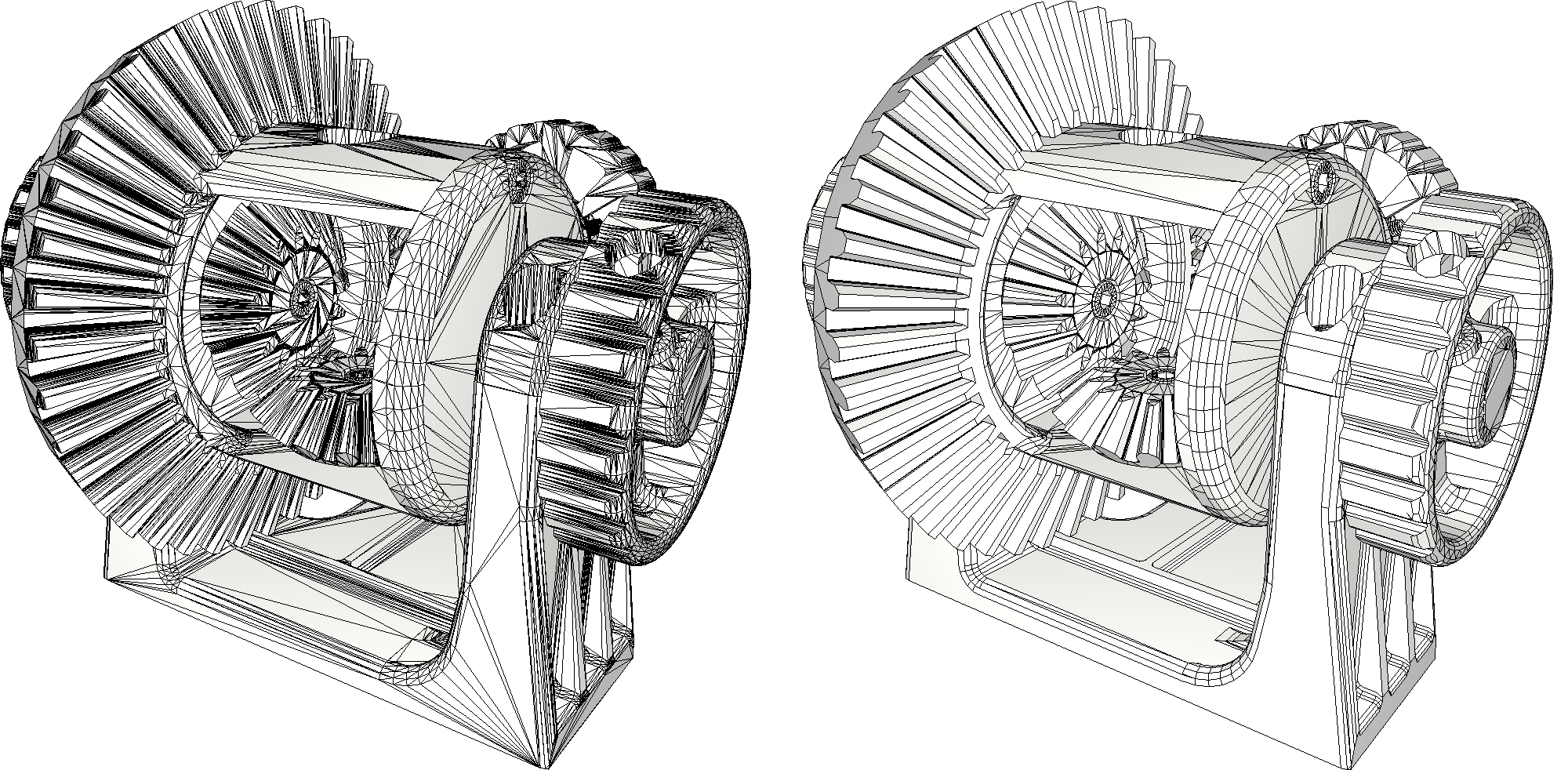
When many triangles are used to describe a planar region of a model, one might wish to simplify the mesh in this region to use as few elements as possible, possibly even a single large polygonal face. This can be achieved using the function CGAL::Polygon_mesh_processing::remesh_planar_patches(). This function performs a detection of the planar regions using geometric predicates for coplanarity and collinearity checks.

Remeshing of a complex mechanical piece.

In real life, models often exhibit slight noise, which might cause regions to be unexpectedly small when using exact predicates because faces are not exactly coplanar. To palliate this, it is possible to specify a threshold on the angle between adjacent faces (resp. segments) such that they are considered coplanar (resp. collinear). Individual functions are also provided for the different steps of the remeshing process (detection of the planar regions, detection of the corners, ...) to enable fine tuning of the algorithm and customization with user-specific criteria.

Status

All these additions are already integrated in CGAL's master branch on the CGAL GitHub repository. Planar Remeshing has been available since CGAL 6.0, and ACVD Remeshing will be officially released in the upcoming version of CGAL, CGAL 6.1, scheduled for mid 2025.

Bibliography

[1] Valette, S., & Chassery, J. M. (2004, September). Approximated centroidal voronoi diagrams for uniform polygonal mesh coarsening. In Computer Graphics Forum (Vol. 23, No. 3, pp. 381-389). Oxford, UK and Boston, USA: Blackwell Publishing, Inc.
[2] Audette, M., Rivière, D., Ewend, M., & Valette, S. (2010, September). Approach-guided controlled resolution brain meshing for fe-based interactive neurosurgery simulation. In Workshop on Mesh Processing in Medical Image Analysis.
[3] Valette, S., Chassery, J. M., & Prost, R. (2008). Generic remeshing of 3D triangular meshes with metric-dependent discrete Voronoi diagrams. IEEE Transactions on Visualization and Computer Graphics, 14(2), 369-381.