Sébastien Loriot & Léo Valque
GeometryFactory
The second half of the work described in this post (snap rounding strategies) will be presented at SGP 2025 in Bilbao (June 30 - July 4, 2025)
Self-intersections in triangle meshes are a common source of issues in geometry processing, simulation, and 3D printing. Such defects can arise in various ways: poor design, approximate conversions, faulty outputs of mesh processing algorithms, and so on. A particularly interesting case in the latter category is Boolean operations, as these turn out to be both a source of self-intersections and, as we will see, a solution to them as well.
Over the years, CGAL has developed its own algorithms for Boolean operations, evolving from general and robust methods to more specialized and efficient solutions (an exhaustive history can be found at the end of this post). To perform robustly, these methods all rely on exact constructions, meaning the use of arbitrary precision numbers (see also the page The Exact Computation Paradigm ). Unfortunately, when results are brought back to the real, double-based world, self-intersections may appear.
Resolving self-intersections in triangle meshes can be tackled in different ways (vertex displacement, complete remeshing, etc.), but these solutions have limitations in terms of scope, computational requirements, or robustness on large datasets.
In CGAL 6.1, we introduce a new method for resolving self-intersections in triangle meshes and triangle soups, combining a novel Boolean operation function called "autorefinement" and a new iterative snap rounding strategy. This approach was evaluated on the Thingi10k dataset (nearly 10,000 models including for non-manifold and degenerate inputs) and produced intersection-free outputs for all cases, thus providing a practical way to address self-intersections in meshes for a wide range of applications.
First Half of the Solution: Autorefinement of Triangle Soups
A question often asked by users was whether CGAL's Boolean operations (see Corefinement and Boolean Operations") could be used to resolve self-intersections in triangle meshes, especially in solids. This led us to modify the corefinement code to create an autorefinement version, which refines triangles from the same mesh that are intersecting along segments not in the input. Using those intersection edges, it is now possible to apply a self-union to resolve the self-intersections of the solid.
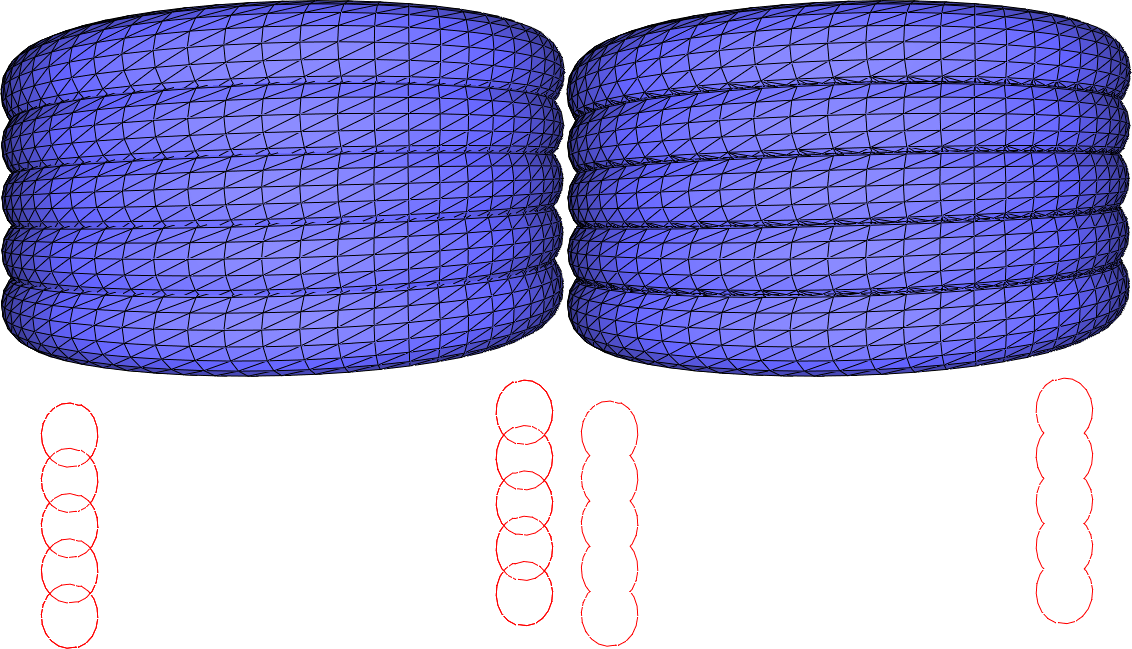
Left: A triangle mesh generated by sweeping a circle along a spiral curve; Right: A triangle mesh free from self-intersection bounding the same volume as in the left picture; On the bottom, we see the intersection curve of a plane with the triangle meshes.
Autorefinement is now available in a new function, CGAL::Polygon_mesh_processing::autorefine_triangle_soup(). This function takes as input a triangle soup (that is, a range of points and a range of triples of integers representing triangles using point indices), and resolves all intersections among the triangles by refining the triangles so that no triangle intersects except along a shared edge or a shared vertex. The function operates on a triangle soup and not a triangle mesh as to handle arbitrarily complex inputs (including degenerate faces and non-manifold configurations), and also to represent non-manifold output. Indeed, even configurations as simple as two triangles whose intersection is a segment will result in four triangles sharing the same edge after refining them with their intersection.
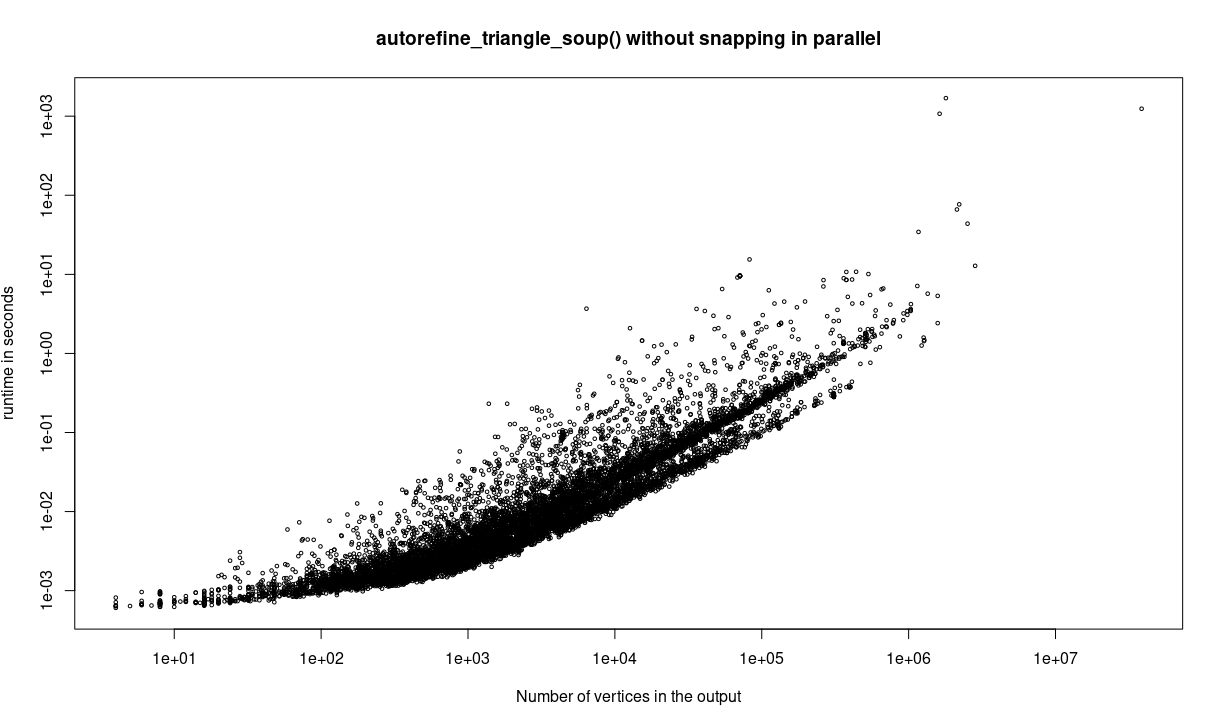
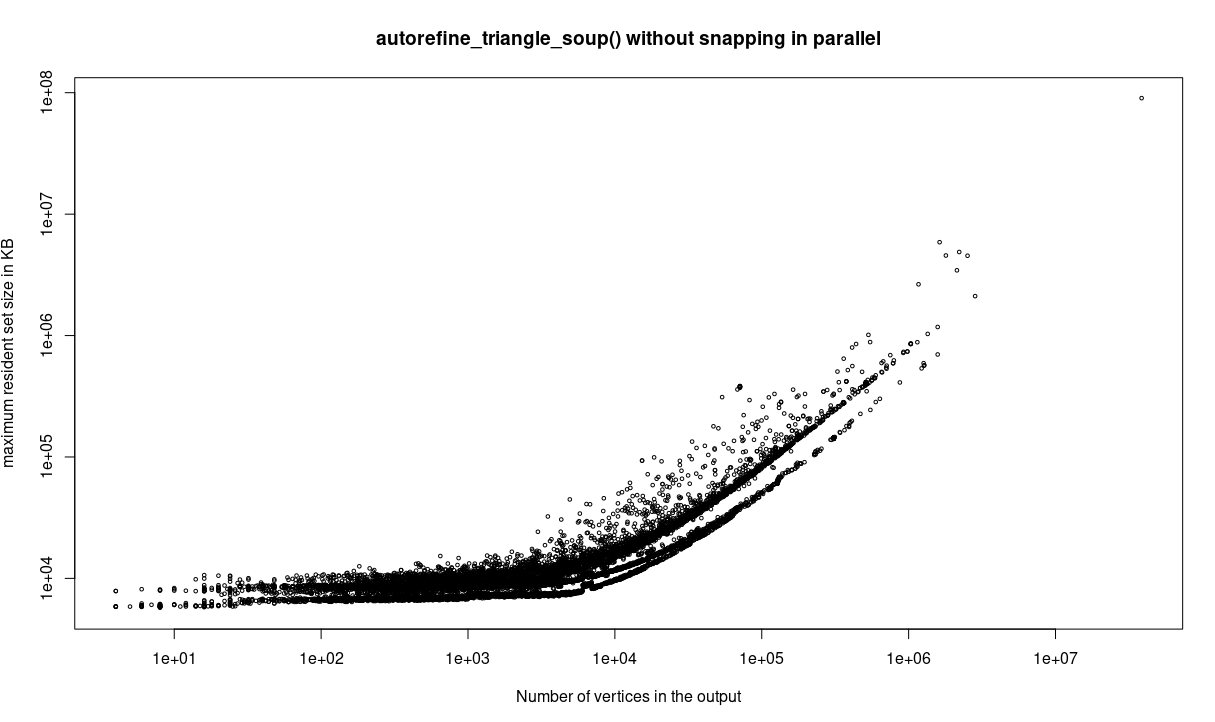
To demonstrate the robustness and runtime efficiency of the function, we ran it over all 10,000 models from the Thingi10k repository. The computer used for the benchmark runs x86_64 Debian GNU/Linux 6.1.0-12-amd64 and features a 2016 Intel(R) Xeon(R) CPU E5-1650 v4 @ 3.60GHz with 6 threads/12 hyperthreads. The memory values are the maximum resident set size (given using the /usr/bin/time command).
Second Half of the Solution: A New Snap Rounding Strategy
Naturally, the new autorefinement function does not suffice by itself to resolve self-intersections as it suffers from the same issues as other Boolean operations: it must be performed using exact computations, but once newly created vertices are rounded back to doubles, self-intersections may appear: out the 9997 valid input files, only 9425 were free from self-intersection after autorefine and naive rounding to double. Therefore, we are left with 572 files still featuring self-intersections.
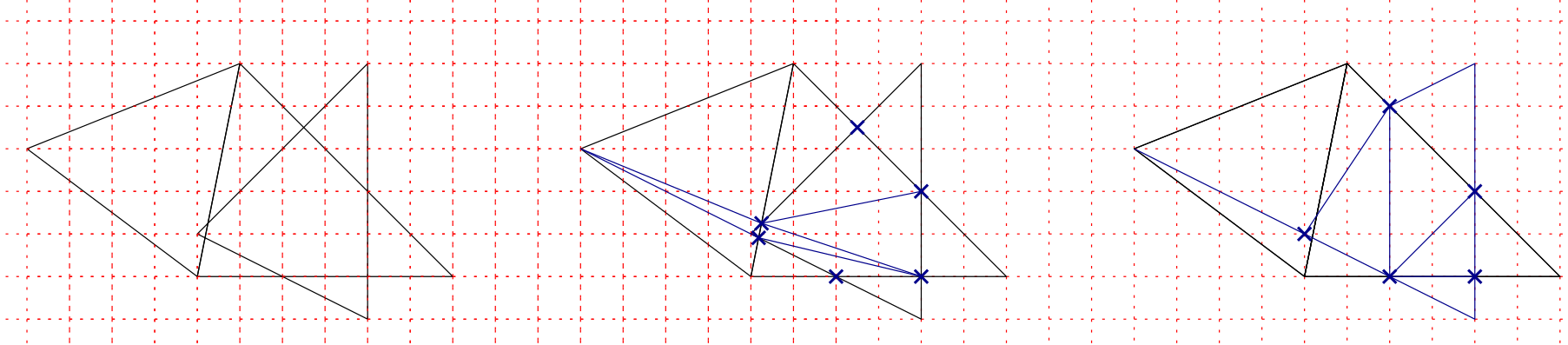
Illustration of rounding issues in self-intersection resolutions. The red grid represent the grid of floating point numbers. Points with floating points coordinates must lie on a vertex of the grid. From left to right: input triangles with floating point numbers coordinates; Resolution of intersections of triangles using arbitrary precision; Rounding new intersection points to the nearest vertex on the grid: even if the intersection is solved with arbitrary precision, the rounding using floating point coordinates induces new intersections that cannot be solved by naively iterating the process (in addition to creating new degenerate faces).
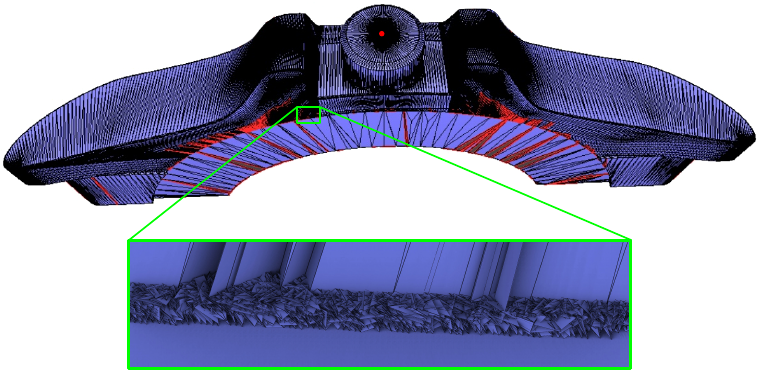
The second part of our solution is a novel snap rounding strategy from Lazard and Valque [1]: the main idea behind the method is a loop that rounds vertex coordinates of triangles involved in self-intersections to integers (up to a scaling factor), eliminates degenerate elements, and resolves self-intersections again, until all self-intersections are resolved or a user-defined maximum number of iterations is reached. Even if there is no theoretical guarantee for successful termination, it performs well in practice: using the default values of the parameters for this method, all the models but one could be rounded with one call. The single remaining model, the infamous model 996816 (see image at the top of the post) required a few more iterations.
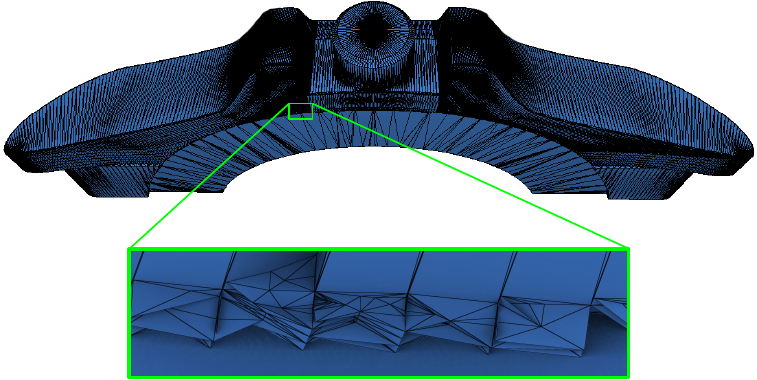
The model 996816 no longer intersects and a reasonable number of new vertices was needed: the input has 75k vertices and 170k faces, and the output has 100k vertices and 245k faces.
From an API point of view, the function CGAL::Polygon_mesh_processing::autorefine_triangle_soup()
has a parameter apply_iterative_snap_rounding() called to the autorefine
function to activate a snapping strategy in order to avoid self-intersections produced while rounding the coordinates to double.
Status
The new function is already integrated in CGAL's master branch on the CGAL GitHub repository and will be officially released in the upcoming version of CGAL, CGAL 6.1, scheduled for summer 2025.
Documentation of the function CGAL::Polygon_mesh_processing::autorefine_triangle_soup()
CGAL master branch on GitHub
Bibliography
[1] Sylvain Lazard and Leo Valque. Removing self-intersections in 3D meshes while preserving floating-point coordinates. Computer Graphics Forum. Vol. 44. No. 5. 2025.
Bonus: History of 3D Boolean Operations in CGAL
In December 2004, CGAL 3.1 was released with the package 3D Boolean Operations on Nef Polyhedra It provided a robust way to compute Boolean operations on Nef Polyhedra. In particular, it enables users to perform some Boolean operations on solids bounded by surface meshes, but also on models with non-manifold features and 1D features. Even today, this package is probably the only solution in the open source world to allow this kind of operations. Unfortunately, all this genericity comes at a price. Indeed, the algorithm relies on maintaining an arrangement of circles on a sphere at each vertex of the Nef Polyhedra in order to enable those operations. This representation also requires that intersection points are strictly coplanar with the polygonal faces they describe, implying that a Kernel providing exact constructions is mandatory.
As this genericity is not required for all applications, we decided to work on an alternative method which would be restricted to solids bounded by triangle meshes, and such that the output is manifold. In October 2012, we released an undocumented version of a new code based on corefinement of triangle meshes. With feedback from early adopters, we officially released with CGAL 4.10 in May 2017 a rewrite of the original 3D Boolean operations through corefinement (see the manual entry "Corefinement and Boolean Operations"). One of the key features of this code is the ability to compute several types of Boolean operations in one run (union and intersection, for example), and the possibility to store the result in a new mesh or directly update one of the input meshes to avoid recopying the entire mesh if only a small portion is affected. When it comes to robustness, exact constructions are used under the hood to guarantee an output with the correct topology. To demonstrate the robustness and speed of the method, we posted a benchmark on the Thingi10k data set testing the code on thousands of models.
In CGAL 4.11 (April 2018), we released an undocumented version of the autorefinement code. The code was, however, limited to meshes where only pairs of triangles were intersecting along the same segment (as an underlying requirement of the code is a pairwise intersection). In order to officially release that code, we needed to overcome this limitation. In 2023, we found the time to start a new implementation from-scratch of autorefinement for triangle soups, which was then peer reviewed in 2024 and officially released with CGAL 6.0 in September 2024.