If you wish to apply, please provide the following information by email to "gsoc-cgal@lists-sop.inria.fr"
Quality Rendering through Ray Tracing
Contact: Pierre Alliez and Stephane Tayeb from INRIA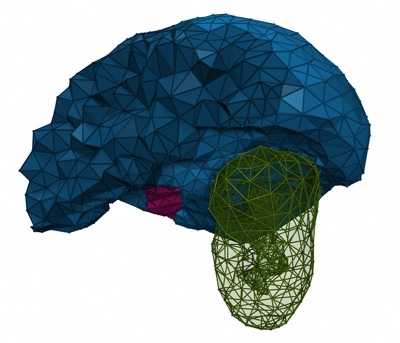
Description:
PhotoRealistic RenderMan (PRMan for short)
and Mental Ray
are de facto standards for generating high quality images by ray tracing, and very good
open source RenderMan implementations such as Aqsis or
Pixie exist.
The goal is to elaborate upon a CGAL C++ rendering component devoted to the generation of
RenderMan files from 3D scenes composed of 3D CGAL objects. The motivation is
to enable the user of CGAL 3D demos to generate for a given camera viewpoint
high definition images with complex transparency and lighting effects. One example motivation
is the rendering of tetrahedron meshes with glass material for the facets and silver
cylinders for the edges to reveal the internal structure of the mesh. Another motivation
is the rendering of 3D point sets with normal attributes.
One part of the component will handle the camera and world placement from the QGLViewer arcball chosen
for the 3D demos of CGAL so that the viewpoint and frustum of the ray-traced images match
the ones of the demos (the idea is to make a ray-traced snapshot of the current scene).
Another part will generate 3D scenes from all 3D finite objects
of CGAL such as triangles, segments, tetrahedra, points, iso cuboids and spheres. As the
point, resp. line primitives are rendered by spheres, resp. cylinders, some options must
be provided to tune the radii. Finally, the component will contain a few functions to facilitate
the selection of materials, transparency and lights for collections of primitives.
Required skills: Templated C++, hands on experience with ray tracing,
knowledge in graphical projection and camera models and taste for computer graphics.
Oracles for Subdivision Surfaces
Contact: Pierre Alliez from INRIA
Description:
If you type "Ray Tracing Subdivision Surfaces" or " Packet-based Ray
Tracing of Catmull-Clark Subdivision Surfaces" in Google scholar you will find a series of papers
which propose solutions to the problem of ray tracing the limit surface of a subdivision algorithm
applied onto coarse control meshes. For surface or volume mesh generation CGAL uses a generic
interface where the input domain boundary is only known through simple intersection tests with
3D segments, lines or rays. The goal of this project is to implement intersection oracles for
the Loop and Catmull-Clark subdivision schemes for which closed form formulas exist
for evaluating their limit surfaces (see article: Charles Loop and Scott Schaefer.
"Approximating Catmull-Clark Subdivision Surfaces with Bicubic Patches".
ACM Transactions on Graphics, Vol. 27 No. 1 Article 8. March 2008).
The goal is to mesh the limit surface of a subdivision
surface applied to very coarse control meshes without having to perform the
subdivision itself.
Required skills: Templated C++, subdivision surfaces and taste for reliable
geometric computing.
Improved 3D convex hull
Contact: Olivier Devillers from INRIA
Description:
The current implementation of 3D convex hull is a bit slower
than 3D Delaunay triangulation and 10 times slower than 2D Delaunay triangulation.
The aim of this work is to improve the current performances of the current 3D convex hull.
This can be achieved through the use of 3D triangulation for dynamic
3D convex hull (and not Delaunay triangulation as suggested in the current manual),
and the use of 2D Triangulation (non Delaunay) for the maintenance of upper and lower hull for incremental 3D convex hull.
Required skills: Templated C++ and taste for computational geometry!
Modular GCD for multivariate polynomials
Contact: Michael Hemmer
Description:
Based on the package Modular Arithmetic the current implementation of the gcd in the Polynomials package already provides a modular gcd for univariate polynomials. However, the implementation for multivariate polynomials only profits from this in the sense that the modular arithmetic is applied in the last step of the recursion, that is, within the computations for univariate polynomials. This was caused by the fact that the current implementation was more focused on the support of polynomials over certain algebraic extensions.
The fundamental structure of the algorithm is as follows. The algorithm proceeds in rounds. In each round it selects a prime and maps the coefficients of the input polynomials in the corresponding prime field. Over this field the gcd is computed using the Euclidean Algorithm. This is repeated until the actual gcd can be recovered using the Chinese Remainder Theorem. This method is more efficient than a naive application of the Euclidean Algorithm since it avoids the exponential coefficient growth in intermediate expressions.
The first milestone of this project is to provide a modular gcd for multivariate polynomials over the integers. This implementation should be compared with existing implementations. We consider this implementation as the default implementation for CGAL. In case CGAL is configured with other libraries that provide a better gcd the code should automatically switch to a better implementation.
A second possible milestone is the support of polynomials over algebraic extensions fields. A fundamental difference to polynomials over integers is that the gcd is not performed over a Field since the extensions may induce zero divisors. This requires special handling within the code and may even effect the current design of the current Number Type Support and Algebraic Foundations of CGAL.
Required skills: Templated C++ and a little bit of algebra.
Allowing different random number generators to be used in CGAL
Contact: Fernando Cacciola
Description:
CGAL provides the class
CGAL::Random
for generating seeded random values via the srand function of the C standard library. This class is
used as the random number generator in some algorithms like the
random geometric object generators.
Since all those random generator functions take an instance of class CGAL::Random it is not possible to choose different distributions (the class doesn't allow that).
The goal of this project is to extend the API of the random geometric object generators to accept other underlying random number generators, such as those from
the Boost.Random library or the upcoming std::random in the next C++ standard, C++0x.
The tasks involve: (1) identify all places within CGAL that use CGAL::Random, study their requirement and elaborate the necessary new concepts,
(2) compare the required concepts with those in Boost.Random and std::random to design interoperability strategies, (3) modify the functions
to accept a parameterized (template) random number generator (of the appropriate concept), instead of an instance of CGAL::Random.
Required skills: Templated C++ and knowledge of concept based design.
Replacing some basic non-geometric tools in CGAL by Boost/TR1/C++0x functionality
Contact: Sylvain Pion from INRIA
Description:
The CGAL project started in 1996, before the
first C++ standard was released, and before the Boost
project was launched. CGAL has accumulated a number of geometry-independent tools
which these days offer duplicate functionality with what is (a) in TR1, (b) planned for
the next C++ standard C++0x, and/or (c) are in Boost. Doing the replacement would help
in the long-term by easing maintenance : (a) less code to maintain, and (b)
new people are more likely to know about a standard tool, and it will be
more useful to them to learn about them, rather than something
which is only in CGAL and with no geometric or scientific flavor.
The goal of this project would be to "cleanup" CGAL by replacing as many of these as possible.
Of course, depending on the case, there can be constraints in terms of efficiency,
API compatibility, deprecation paths, etc. So, the task is non trivial,
but there are pieces easier than others. It should be a nice way to learn about various
standard tools in CGAL, Boost and C++0x.
Some examples of things to be considered :
Filter_iterator -> boost::filter_iterator
Object -> boost::any/variant
Triple/Quadruple -> TR1::tuple/array
Unique_hash_map -> TR1::unordered_map/set
copy_n -> C++0x::copy_n
iterator ranges -> Boost.Range
Timers -> Boost.Timers
Integer8/16/32 -> int32_t...
min_max_element -> C++0x (or TR1 ?)
predecessor/successor -> prev/next (C++0x/TR1)
Note that there is a separate project idea for Random Numbers generators.
Required skills: C++, templates.
Standard File Format readers/writers
Contact: Pierre Alliez from INRIA
Description:
CGAL interacts with other systems dealing with geometric data sets.
These can be simple point sets ("xyz"), surface meshes (OFF, OBJ, PLY), volume meshes (ABAQUS, etc)
or more involved CAD/CAM file formats (DXF, STL). There are already a few file
format readers and writers in CGAL.
The goal of this project is to obtain a nice collection of high-quality readers/writers for
standard file format. They would be usable independently of CGAL data structures and algorithms,
but with a C++ interface which will make them easy and natural to use with CGAL algorithms.
The first task will consist in precisely identifying the standard file formats which exist
for dealing with geometry, then see which are already used in CGAL, or potentially useful
for CGAL to support.
Then, the work will consist in designing the interface of the parsers, based on the needs
of current use in CGAL, and then implementing them, together with their documentation.
To start with priority will be given to surface and volume meshes.
Finally, as time permits, updating the CGAL code to use these might be nice!
Required skills: C++, templates, parser tools (Boost.Spirit
maybe ?), some ideas of what geometric data is about, but no a priori
knowledge of geometric algorithms is needed.
A VTK Interface for CGAL components
Contact: Andreas Fabri from Geometry Factory
Description:
VTK is an object-oriented software system for computer graphics, visualization, and image processing. VTK has the
notion of a graphics pipeline. There are two basic types of objects involved: data objects and process objects,
and compatible objects can be assembled in a pipeline with setInput and getInput methods.
The goal of this project is to wrap the CGAL algorithms, starting with the CGAL surface and volume mesh generators for 3D images, so that they
become VTK process objects which fit in the VTK graphics pipeline, without that VTK users have to learn CGAL.
Required skills: C++, VTK.
A web service that solves geometric problems.
Contact: Efi Fogel from Tel Aviv University
Description:
Create a web service open to the public that offers solutions to the geometric problem described below. The service should be integrated into this website, which runs Plone (an open source content management system). The service should be designed in such a way that it can easily extend to other geometric problems.
Given a polygonal robot Q, which can translate (but not necessarily rotate) in a room cluttered with polygonal obstacles, maintain a data structure that can efficiently answer queries of the following form: Given a start position s of some reference point in Q and a goal position g, plan a collision-free motion of the robot from s to g.
The feed is done in two steps. First, the user uploads the geometric data that describes the work space. Then, the user uploads the queries in forms of pairs of start and goal positions - a pair at a time. For each pair the geometric description of the collision-free path is computed and offered to the user. The web page can illustrate the workspace, the queries, and the obtained solutions.
The user can choose values for several parameters, such as the quality of the path (e.g., short, high-clearance, shortest subject to prescribed clearance) and whether the robot can touch the obstacles.
Required skills: C++, Plone, and PHP.
The core of the solution should be an application written in C++ based on CGAL arrangements and other CGAL components implementing some motion planning algorithms. The mentor will provide description of the algorithms and code components. An application that solves the most simple variant already exists.
The interface should be through a web page integrated into an existing Plone based website. Basic skill in managing Plone websites is required. We assume that for some desired features some extra skills in Plone and PHP are required as well, although they may be acquired as the project advances.
Scilab bindings via SWIG
Contact: Sylvain Pion from INRIA
Description:
This idea is more a collaboration with another software project, also GSOC mentoring organization : the Scilab project. The idea is to revisit the draft interface between those two software, done years ago, but this time using SWIG. Main mentoring would be done within the Scilab project, co-mentored on the CGAL side as well. See here for details.
Towards more parallelism in CGAL triangulations and meshes
Contact: Sylvain Pion from INRIA
Description:
Algorithms in CGAL are currently essentially sequential. Some work has begun on parallelizing the computation of Delaunay triangulations, but a lot remains to be done, in various areas. Students can propose important areas that they think they could parallelize.
Triangulation_3 demo
Contact:
Manuel
Caroli and
Monique
Teillaud from INRIA
Description:
The goal is to implement a demo program for the
Triangulation_3
package using Qt and the QGLViewer. The
Triangulation_3 package contains algorithms for computation of
Delaunay triangulations and weighted Delaunay triangulations for a
given point set. We aim for an interactive demo that illustrates
the package functionality and the used algorithm. So far the 3D
demos in CGAL allow for very little interaction. We expect the
participant to come up with a nice and easy-to-use mode of
interaction that can possibly be reused by other demos in the
future.
A first milestone could be a non-interactive demo that contains all
the functionality. A second milestone would be to add the
interactivity.
Required skills: C++, a little Qt and OpenGL
