André Nusser°, Marvin Künnemann†, and Karl Bringmann°;
°CNRS / Inria Center at Université Côte d’Azur, †Karlsruhe Institute of Technology, *Max Planck Institute for Informatics
The Fréchet distance is a classical dissimilarity measure between polylines. Intuitively, the Fréchet distance is commonly explained as follows: Imagine a human walking on one polyline while a dog walks on the other polyline, they are connected by a leash, and they are only allowed to walk forward. The Fréchet distance is the shortest leash length that allows the human and the dog to jointly walk from start to end on their respective trajectories where they can each vary their speed arbitrarily. The Fréchet distance has significant advantages over other measures because it considers the polylines as continuous objects and takes into account the ordering of the points.
The applications of this distance measure are plenty, for example:
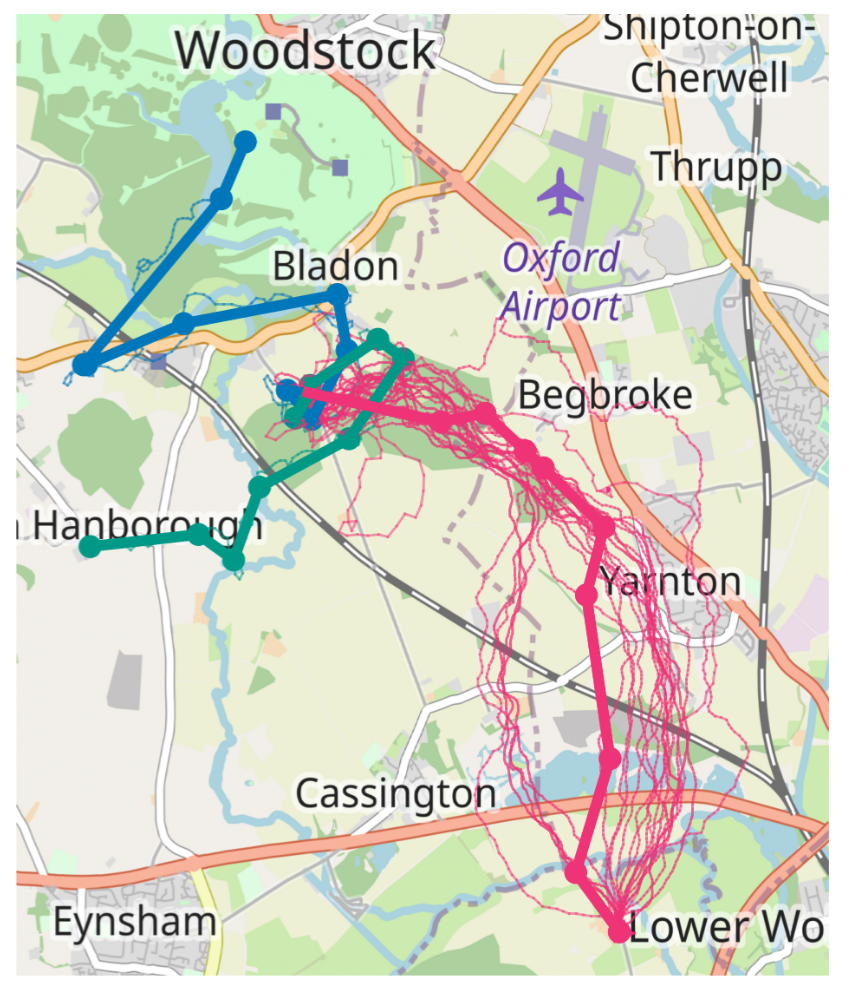
- Comparing the GPS traces of migrating animals to find the different routes that are being used;
- Measuring the similarity between movement patterns recorded via motion capture;
- Perform map matching to match a GPS trace to a transportation network.
Frechet distance is a powerful tool to compute clusters of given polylines [1, Fig. 1]
New Package: dD Fréchet Distance
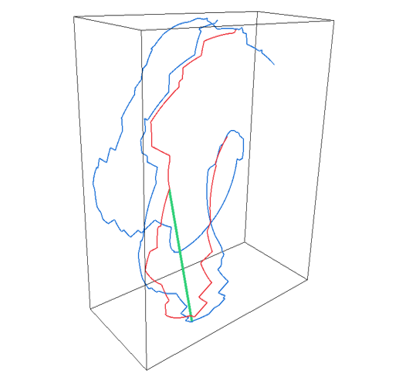
This new package provides the means to compute a bounded approximation of the Fréchet distance between two polylines, as well as a near neighbor data structure for polylines under the Fréchet distance, both in d-dimensional Euclidean space.
The following code snippet demonstrates how to compute the Fréchet distance between two polylines, with a maximal error of 0.000001 to the exact distance:
std::vector<Point> pA, pB;
CGAL::IO::read_linestring_WKT("wkt/moebius.wkt", pA);
CGAL::IO::read_linestring_WKT("wkt/moebius2.wkt", pB);
std::pair<double, double> res = CGAL::bounded_error_Frechet_distance(pA, pB, 0.000001);
std::cout << "The Frechet distance between the polylines is between " << res.first << " and " << res.second << std::endl;
The two polylines (blue and red), and the a visualization of the distance (green).
Fast and Correct
Following the usual Exact Computation Paradigm,
this package guarantees the correctness of the result, provided functions are called using a kernel offering
filtered predicates or exact predicates, such as provided by the kernel CGAL::Exact_predicates_and_inexact_constructions_kernel.
The implementation is based on a series of state-of-the-art papers by Bringmann et al. [2, 3], which significantly improved on previous state of the art. Furthermore, the algorithm is not concerned by the curse of dimensionality. We refer to the papers themselves for a very detailed practical analysis.
Status
The package Fréchet Distance has been available since CGAL 6.1, released in the fall of 2025.
Documentation of the “dD Fréchet Distance” package
CGAL “main” branch on GitHub
Bibliography
[1] M. Brankovic, K. Buchin, K. Klaren, A. Nusser, A. Popov,and S. Wong, (k, l)-medians clustering of trajectories using continuous dynamic time warping. In Proceedings of the 28th International Conference on Advances in Geographic Information Systems 2020 Nov 3 (pp. 99-110).
[2] Karl Bringmann, Marvin Künnemann, and André Nusser. Walking the dog fast in practice: Algorithm engineering of the fréchet distance. In Gill Barequet and Yusu Wang, editors, 35th International Symposium on Computational Geometry, SoCG 2019, June 18-21, 2019, Portland, Oregon, USA, volume 129 of LIPIcs, pages 17:1–17:21. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2019.
[3] Karl Bringmann, Marvin Künnemann, and André Nusser. Walking the dog fast in practice: Algorithm engineering of the fréchet distance. J. Comput. Geom., 12(1):70–108, 2021.
